Wavelet Tree for Competitive Programming
最近在学FM-Index相关算法用于数据库,了解到Wavelet Tree这一数据结构,发现其还可以应用在算法竞赛中。网上相关中文资料比较少,权当自己做个学习笔记
开始之前
在学习wavelet tree前,不妨看看他能解决什么样的问题。
假设我们有一长为 $n$ 的序列 $A[0…n - 1]$ 。在算法竞赛中,典型的数据量是 $n = 1e5, |A[i]| <= 1e9$
- 区间 $[L, R)$ 中元素$x$的
出现次数 - 区间 $[L, R)$ 中的
第k小数 - 区间 $[L, R)$ 上
小于等于x的数的个数 - …
以上问题都可以通过可持久化线段树在解决。那为什么还需要wavelet tree呢,我们都知道可持久化线段树的常数很大,并且十分消耗空间,在有些苛刻的题目下可能会被卡 好吧应该都是金牌题,不是我该考虑的 。利用wavelet tree可以在$log(\sigma)$时间内完成的同时(且优秀的常数),若使用bitvector优化空间,空间上大概比可持久化线段树少一个量级。最重要的一点是,我个人觉得他比主席树更加直观易懂。
$\sigma$ = | $\Sigma = {1, 2, \cdots, \sigma}$| (用于序列上时是值域大小)。
用wavelet tree的缺点就是带修改操作比较难写,码量较大,一般不会在比赛时使用。
Wavelet Tree
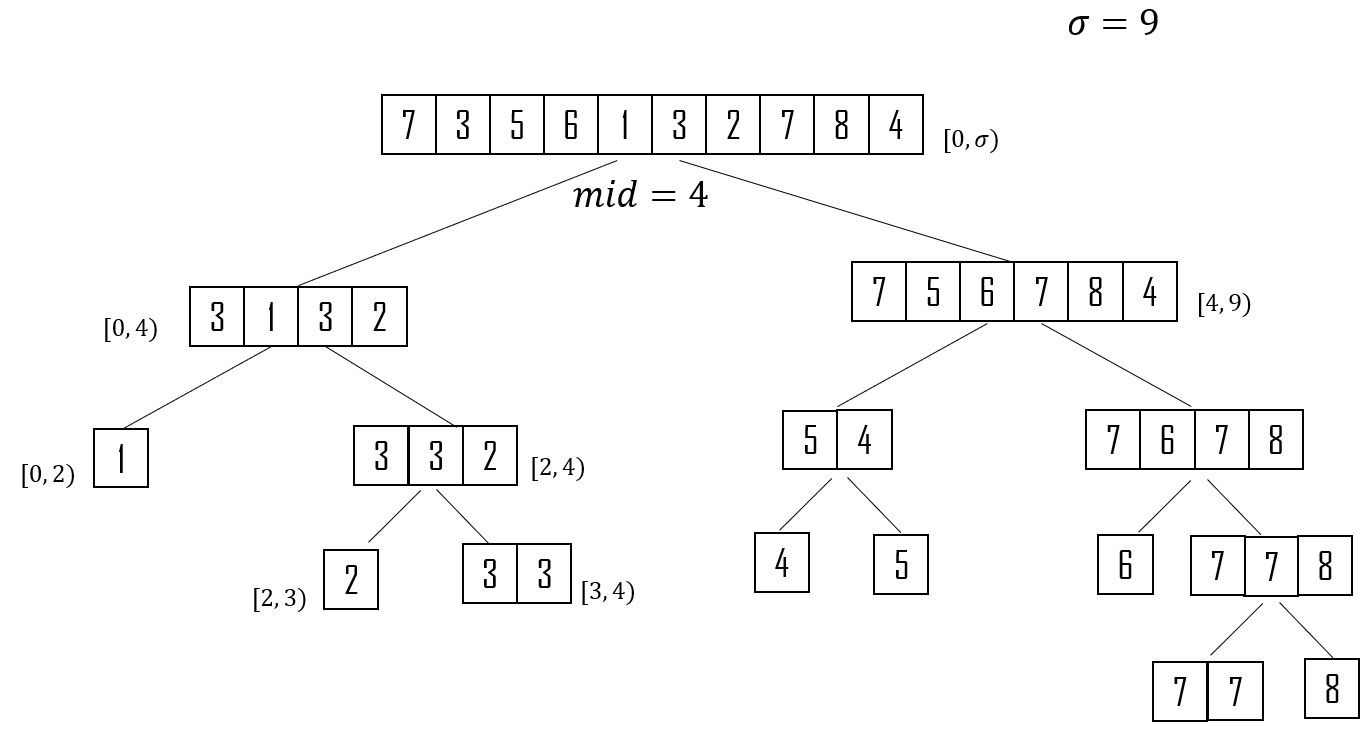
该图给出了用序列 $A = [7, 3, 5, 6, 1, 3, 2, 7, 8, 4]$ 构建的wavelet tree的形态。对于树上的每个节点,我们会将其按照值域分成两个部分$[low, mid), [mid, high)$。通过 稳定划分(stable_partition,即不改变相对顺序的情况下划分)将该节点上的序列中小于 $mid$的划分到左子树中,大于等于mid的划分到右子树中,递归直至节点中只有一种值时为叶节点。需要注意的是,我们并不会在叶子节点中直接存储序列的值,而是通过某个方法使得我们能够使用较小的空间的情况下得到足够的信息。
设根节点编号为 $u = 1$ ,其左子树的根节点为 $2 * u$ , 右子树的根节点为 $2 * u + 1$ ,以此类推。每个节点都对应一对左闭右开的区间 $[lo, hi)$,表示该节点中数值的值域范围。同时有一个 $mid = \lfloor \frac{lo + hi}{2} \rfloor$ ,表示该节点左右子树分裂标准,即左子树中值域范围是 $[lo, mid)$ , 右子树 $[mid, hi)$ 。
在wavelet tree中,我们实际上在维护一个二维数组vector<vector<int>> c,我们不妨叫他前缀计数数组,其中 c[u][i]表示的是u结点中下标为[0, i)中的数有多少个小于该节点对应的mid。另外,若$u$结点中有$n$个数,那么c[u].size() = n + 1, 我们另c[u][0] = 0。例如,下图给出了部分结点对应的 c[u][i]数组

现在,我们来看如何用这个构建好的前缀计数数组完成以下的查询问题:
rank(int val, int pos)
该函数返回区间 $[0, pos)$ 中值为$val$的数的个数(我也不知道为什么叫rank。。。或许这个名称是由bitvector中继承而来?)。有了这个函数,我们就容易得到区间 $[i, j)$ 内某个数的出现次数,就是 $rank(val, j) - rank(val, i)$
设 $rank_u (val, pos)$ 为结点$u$中值为val的数在 $[0, pos)$ 中的出现次数( $pos <= size(u)$ )$mid$为节点$u$分裂标准,我们可以得到:
- 若 $val < mid$,则 $rank_u(val, pos) = rank_{LeftChild(u)}(val, c[u][pos])$
- 若 $val >= mid$, $rank_u(val, pos) = rank_{RightChild(u)}(val, pos - c[u][pos])$
如何理解上述变化呢,其实也很简单,就是要理解c[u][i]的意义,它同时也表示将u结点中下标为i的点映射到子结点中后他的位置。而映射规则为若这个数小于mid,则将其映射到左儿子的c[u][i]处;若这个数大于等于mid,则将其映射到右儿子的i-c[u][i]处 不理解的可再仔细想想c[u][i]的这两个解释之间的等价性。
有了上述说明,我们就容易递归的完成$rank$操作。例如,假设我们需要得到 $rank_1(val = 3, pos = 7)$ -由于 $3<mid,c[1][7] = 4$, 则递归左子树 $rank_2(3, 4)$;
- 左子树中,$3 >= (mid = 2), 4-c[2][4] = 3$,递归到右子树 $rank_5(3, 3)$
- 右子树中,$3 >= (mid = 3), 3-c[5][3] = 2$,递归到右子树
- 右子树为叶子节点,则此时结点内的树的个数(即为上一步中 $3-c[5][3] = 2$)为$val$的个数
quantile(int k, int l, int r)
该函数返回区间 $[l, r)$间的第k小数(最小的为第一小)。我们知道,c[u][l]表示下标为结点 $u$中有多少个下标在 $[0, l)$中的数被映射到了左子树。那么,
- 若
c[u][r] - c[u][l] >= k,则区间 $[l, r)$内第k小即为左子树中的第k小。 - 若
c[u][r] - c[u][l] < k,则区间 $[l, r)$内第k小即为右子树中的第k - (c[u][r] - c[u][l])小。
从而我们可以递归的进行求解。
c数组的构建
实际上上面已经讲的差不多了,直接看代码:
// 参数都是该结点对应序列相关
// u: 该结点编号
// begin, end: 该结点对应序列的首个,末尾迭代器
// lo, hi: 该结点对应值域为 [lo, hi)
void build(iter begin, iter end, int lo, int hi, int u) {
if(hi - lo == 1) {
return;
}
int m = (lo + hi) / 2;
c[u].reserve(end - begin + 1); // reverse只分配空间不进行构造,所以后面还可以push_back
c[u].push_back(0);
for (auto it = begin; it != end; ++it) {
c[u].push_back(c[u].back() + (*it < m));
}
// 稳定划分,将[begin, end)间的小于m的值划分到前半部分,pivot为后半部分首个迭代器
auto pivot = stable_partition(begin, end, [=](int i){return i < m};);
build(begin, pivot, lo, m, 2 * u);
build(pivot, end, m, hi, 2 * u + 1);
}
到这个,我们已经可以利用没有进行空间优化的wavelet tree轻松切掉这道 可持久化线段树的模板题了,代码如下
模板
#include <bits/stdc++.h>
using namespace std;
struct WaveletTree {
using iter = vector<int>::iterator;
vector<vector<int>> c;
const int SIGMA;
WaveletTree(vector<int> a, int sigma): c(sigma*2), SIGMA(sigma) {
build(a.begin(), a.end(), 0, SIGMA, 1);
}
void build(iter begin, iter end, int lo, int hi, int u) {
if(hi - lo == 1) return;
int m = (lo + hi) / 2;
c[u].reserve(end - begin + 1);
c[u].push_back(0);
for (auto it = begin; it != end; ++it) {
c[u].push_back(c[u].back() + (*it < m));
}
auto p = stable_partition(begin, end, [=](int i)
{ return i < m; });
build(begin, p, lo, m, 2 * u);
build(p, end, m, hi, 2 * u + 1);
}
// occurrences of val in position[0, i)
int rank(int val, int i) const {
if(val < 0 or val >= SIGMA) return 0;
int lo = 0, hi = SIGMA, u = 1;
while(hi - lo > 1) {
int m = (lo + hi) / 2;
if(val < m) {
i = c[u][i], hi = m;
u = u * 2;
} else {
i -= c[u][i], lo = m;
u = u * 2 + 1;
}
}
return i;
}
// get kth smallest number in [l, r)
int quantile(int k, int l, int r) const {
// assert(k > 0 && k <= j - i);
int lo = 0, hi = SIGMA, u = 1;
while(hi - lo > 1) {
int m = (lo + hi) / 2;
int nl = c[u][l], nr = c[u][r];
if(k <= nr - nl) {
r = nr, l = nl, hi = m;
u = 2 * u;
} else {
k -= nr - nl;
r -= nr, l -= nl, lo = m;
u = 2 * u + 1;
}
}
return lo;
}
};
int main() {
ios::sync_with_stdio(false);
cin.tie(nullptr); cout.tie(nullptr);
int n, q;
cin >> n >> q;
vector<int> a(n);
for (int &x : a) {
cin >> x;
}
WaveletTree wt(a, *max_element(a.begin(), a.end()) + 1);
while(q --) {
int k, l, r;
cin >> l >> r >> k;
l--;
cout << wt.quantile(k, l, r) << '\n';
}
return 0;
}