最近正在学习 MIT 6.5940, 韩松老师的课，做deep learning compression的应该都只知道。课程分为三个部分，efficient inference, domain-specific optimization, efficient training。有完整的课件，视频和实验。最后一个lab是将llama2部署在个人电脑上，非常有意思（谁不想要个自己的大模型呢）。其余lab也都可以白嫖google colab的gpu
Introduction
正式介绍pruning and sparsity之前，我们先来聊聊为什么要做model compression这个事情。
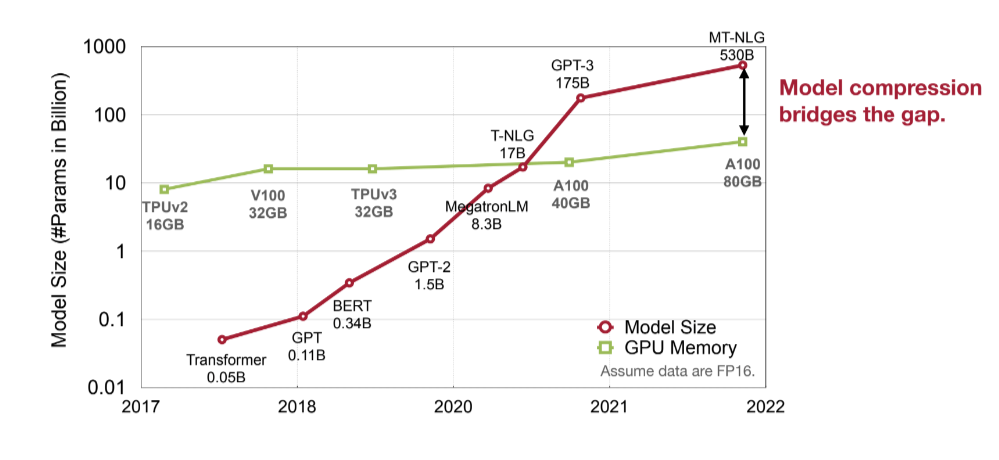
Today’s Model is Too Big!
随着Large language model的出现，如GPT-3，如今的模型参数量已经达到了上百billion，别说训练，我们甚至无法在一个gpu上对其进行推理。更别提如果我们想要将其部署在其他边缘设备上。
所以当前在做inference之前，一般都会有个model-compression的过程，包括pruning（剪枝），quantization（量化），distillation（蒸馏）等。这些方法都是为了减少模型的大小，加速推理过程。这些方法也被广泛地集成到了各种加速卡，gpu中。例如nv的A100就支持structured sparsity（[N:M]形式的，具体含义下文会详细介绍）。
Efficiency Metrics
我们再来看看一些 efficiency metrics，这也是我们在做inference过程中需要考虑的指标：
- Memory-Related Metrics
- # parameters
- model size
- total/peak #activations
- Computation-Related Metrics
- MACs
- FLOP, FLOPs
# parameters
下表是一些常见结构的参数数量：
| Model | #Parameters |
|---|---|
| Linear Layer(FC) | $feature_{in} * feature_{out}$ |
| Conv Layer | $c_{i} * c_{o} * k_{h} * k_{w} $ |
| Grouped Conv Layer | $c_{i} * c_{o} * k_{h} * k_{w} / g$ |
| Depthwise Conv Layer | $c_{o} * k_{h} * k_{w}$ |
其中，Grouped Conv指的是将输入在channel维度进行分组，然后分别进行卷积，最后concatenate。Depthwise Conv是分组个数 $g$ 等于输入channel数的情况。
除了这些weight外，还有bias以及norm相关的参数。 例如，对于batchnorm层，我们需要两个参数$\gamma, \beta$以及runing mean和running variance。 $$ y = \gamma \frac{x - \mu}{\sqrt{\sigma^2 + \epsilon}} + \beta $$
这都是针对infernece的情况，对于training，还需要考虑一些额外的参数，例如momentum，以及保存梯度等等。
model size
$$ Model Size = \# parameters * bitwidth $$
举个例子，AlexNet有$61M$个参数，如果我们用32bit的float来表示，那么model size就是$61M * 4byte = 224MB$。但如果我们用8-bit来表示每个weight，那么model size就是$61M * 1byte = 61MB$。
这就是quantization的一个应用，通过减少bitwidth来减少model size。
total/peak #activations
#activations 是模型在推理时在内存中需要存储的中间结果，这也可能成为内存瓶颈。如下图所示：
该图展示了MCUNet(一个专门用在IoT设备上的模型)的参数量和activations数量对比resnet的减少。可以看出，参数的减少量十分显著，但是# activations不降反增，和param的占比是一个数量级的。所以我们若想在边缘设备上部署模型，需要考虑activations的数量。
MAC
MAC的含义是 Multiply-Accumulate operation。例如，一个gemm(genearl matrix multiplication)的$MACs = m * n * k$（对于m * k的矩阵和k * n的矩阵相乘）。深度学习中几乎90%的时间都在做gemm，一个conv2d操作也可以由im2col转换为gemm操作。
以下是常见的一些layer的MACs计算：
| layer | MACs(batch size = 1) |
|---|---|
| Linear | $feature_{in} * feature_{out}$ |
| Conv | $c_{i} * k_{h} * k_{w} * h_{o} * w_{o} * c_{o}$ |
| grouped conv | $c_{i}/g * k_{h} * k_{w} * h_{o} * w_{o}* c_{o} $ |
| depthwise conv | $c_{o} * k_{h} * k_{w} * h_{o} * w_{o}$ |
（简单解释一下conv2d的MACs：对于每个输出特征图上的每个像素点，都需要进行 $c_i \times k_h \times k_w $ 次乘法运算和累加操作（假设每个卷积核和输入通道的对应部分做完整个卷积运算）。因为输出特征图有 $c_o$ 个通道，每个通道有 $h_o \times w_o$ 个像素点，所以总共的MACs数就是上面公式中的乘积。）
FLOP and FLOPs
FLOP的意思是 Floating Point Operations，是指浮点运算的次数。FLOPs是指每秒的FLOP数量。 一般一个MAC对应两个FLOP，一乘一加。
Energy Consumption
对于边缘设备，我们还需要考虑能耗的问题。
图中可以看出，从内存中取数操作的能耗是运算的200倍以上。
neural network pruning
那么，到底什么是 模型剪枝（model pruning） 呢？顾名思义，就是将模型中的一些参数去掉，或者更加细粒度的，我们可以把某些参数与参数之间的连接去掉。还有一个常用的概念是 稀疏度（sparsity） ，指的是剪枝后的参数占原有参数的比例。例如，如果我们剪去了90%的参数，那么sparsity就是0.1。
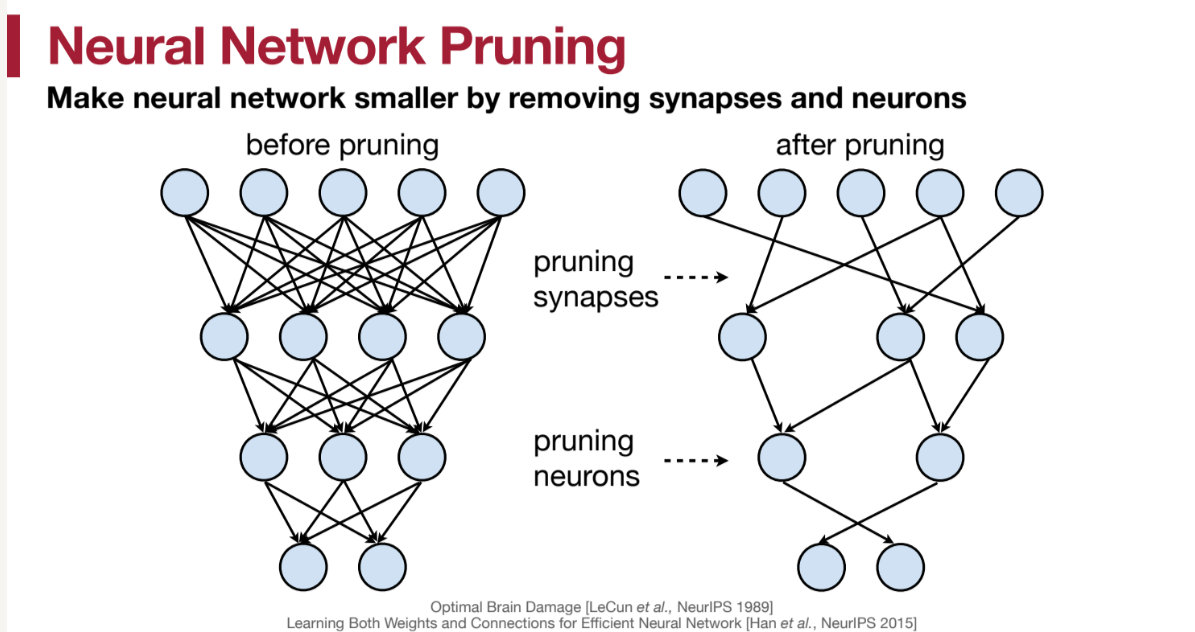
注意：剪去某个参数并不意味着单纯将其设置为0。因为我们剪枝的目的是减少内存使用以及加速推理，若只是讲某个$W$矩阵中的一些值变成0，并不能达到减少内存的目的。我们需要将剪枝后的参数$W_{p}$用特定的方式存储（例如，稀疏矩阵）以及结合特定的优化后的运算才能减少内存使用并加速。当然，从正确性的角度来说，将某些参数设置为0可以得到一样的结果。所以我们可以在确定 sparsity 时先将一定的参数置为0，然后再通过fine-tuning来确定剪去这么多的参数是否会影响模型最终的效果。
减去一定的参数后，肯定会对我们的模型效果造成影响。这时候我们需要进行fine-tuning调整参数分布，具体会在后文展开。
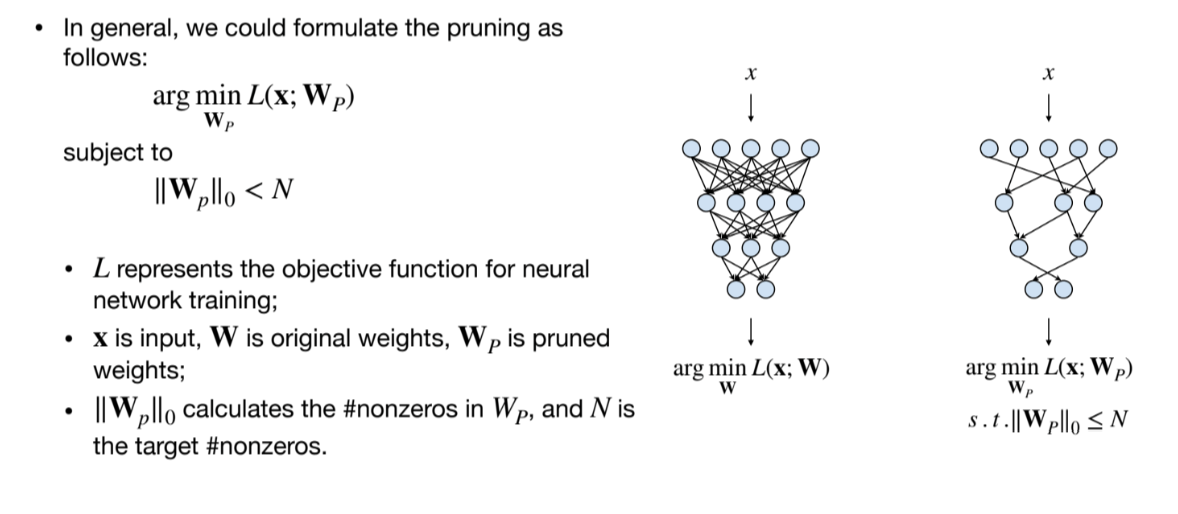
形式化的定义prune：
pruning granularity
我们有不同的剪枝粒度，from unstructured to structured。
对于一个FC layer，其实就是将一个2d matrix进行剪枝：
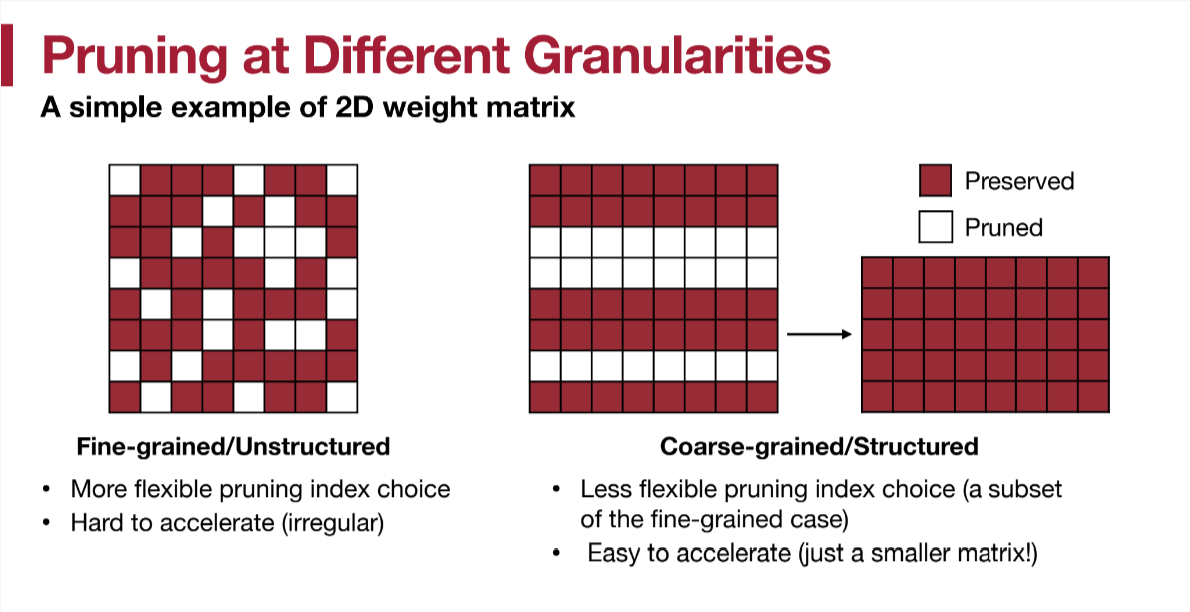如图，细粒度的、不规则的剪枝一般能有更高的sparsity，但是却难以加速（就像上文说的，如果只是将一些参数设置为0，不会有任何内存与速度上的收益）。而粗粒度的剪枝，就可以不需要改变原有的矩阵结构获得更少的内存使用以及加速，但一般sparsity会高一些（同等accuracy下）。
对于卷积层，我们有更多的剪枝粒度：
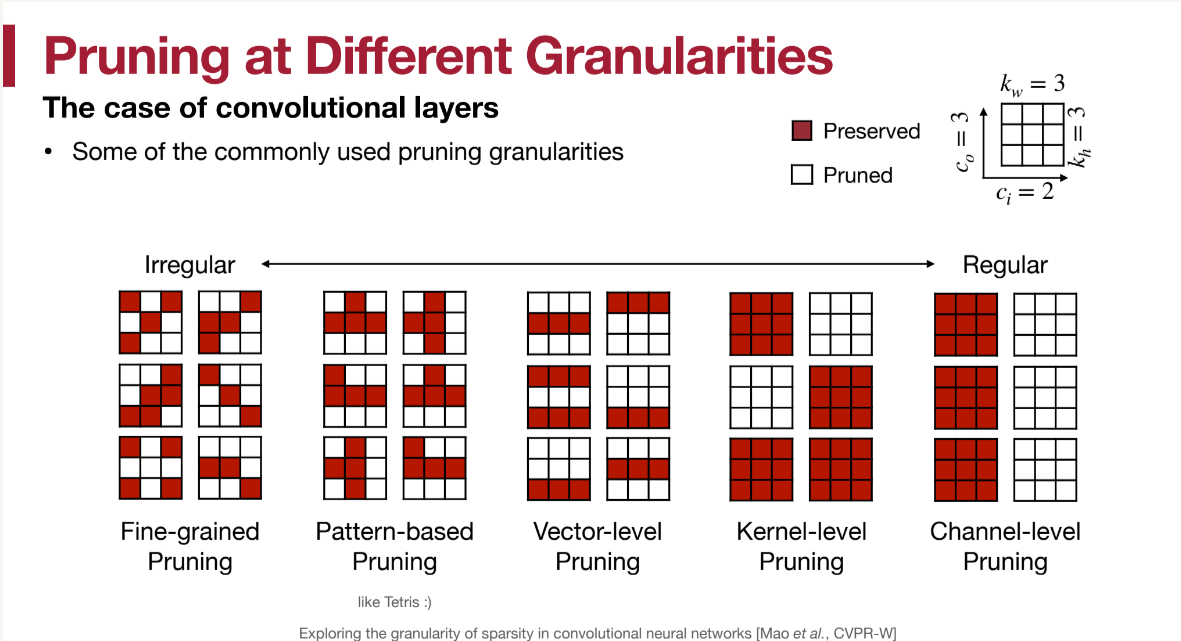也是从完全不规则，到有一定的pattern，到vector-level，kernel-level再到剪去一个通道。优缺点如同上面分析的一般。
对于最fine-grained的剪枝，许多模型都可以达到剪去90%以上而不影响精度。
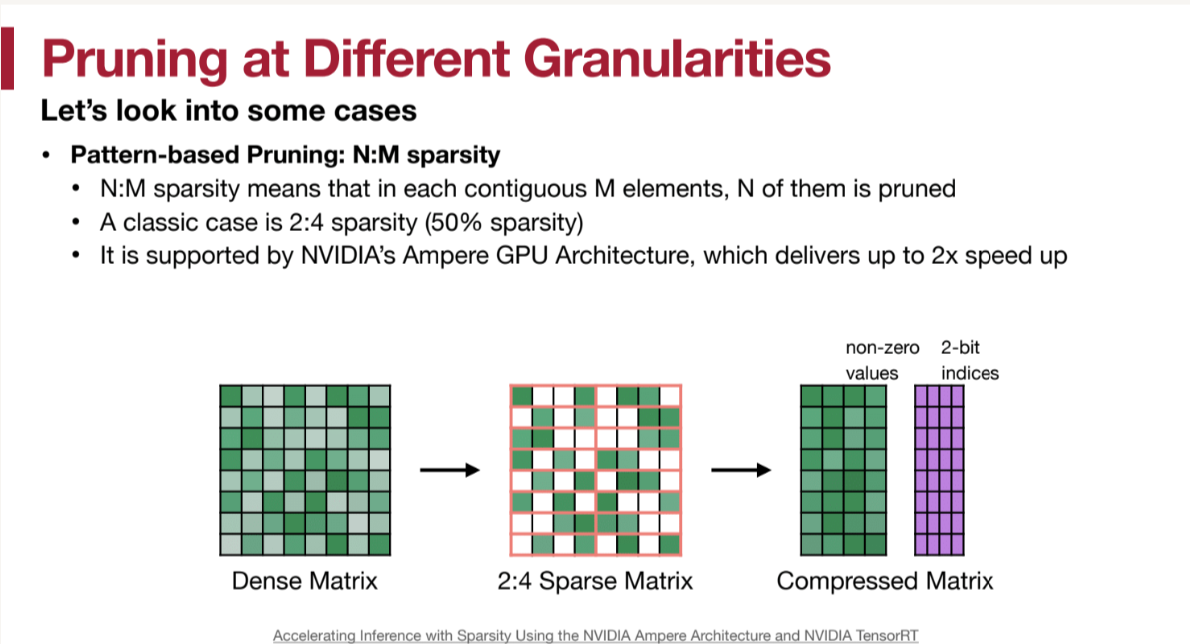
对于有一定pattern的剪枝，就需要设计特定的存储方式或者运算方式来加速。
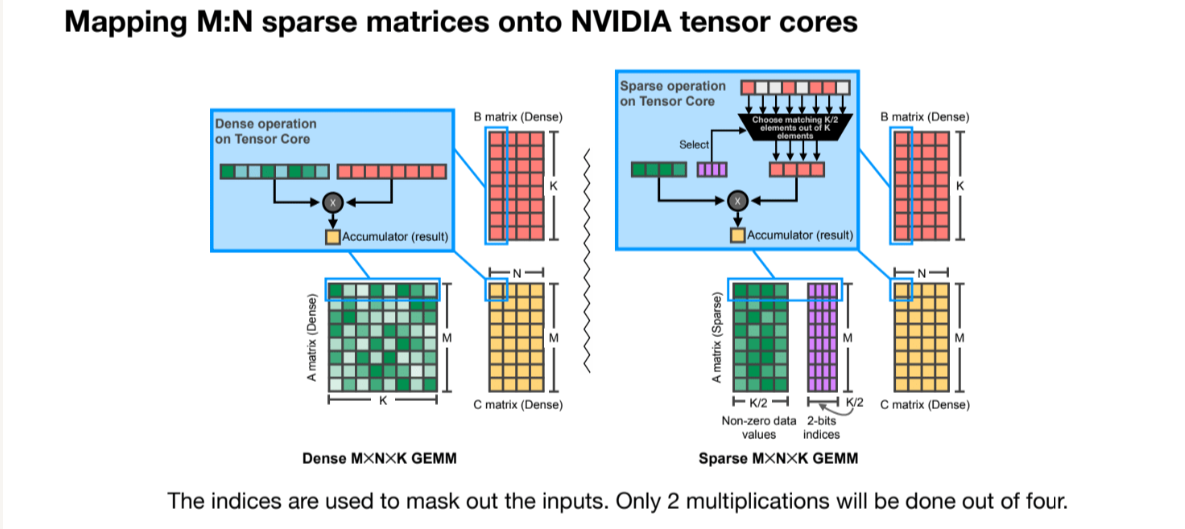
例如下图的[N:M]剪枝（每M个参数剪去N个）就可以通过只存非0权重，以及一个下标数组的方式减少内存占用。nvdia的Ampere系列GPU就在其Tensor core内融合了这种优化，达到了2倍的加速效果
对于conv的剪枝，我们还用的一个不需要硬件特定实现的方法就是直接进行channel-level pruning，也就是直接减去特定的通道。
- pros: 直接的加速，无需特定硬件
- cons: 更少的模型压缩比 不同的卷积层的sparsity又该如何确定呢？是所有卷积层的sparsity都设置的相同还是各不相同？有什么样的标准呢？我们会在在pruning ratio这里会讲到。
pruning criterion
如何确定剪去的权重呢？常见的有magnitude-based pruning，scaling-based pruning等
Magnitude-based pruning
Learning Structured Sparsity in Deep Neural Networks Wen et al., NeurIPS 2016
只得就是通过权重的重要程度来进行剪枝。直觉上看，对于一个激活函数$y = ReLU(10x_0 - 8x_1 + 0.1x_2 )$，肯定是$0.1$这个权重对其结果影响最小，可以将其剪去。 依此定义重要度$Importance = |W|$，直接按照数值的大小进行剪枝。当然，我们也可以将其拓展到任意范数： $$ Importance = |W|p = (\sum{i} |W_i|^p)^{\frac{1}{p}} $$ 只不过最常用的还是l1范数，因为这引入的额外的计算量较小。
Scaling-based pruning
Learning Efficient Convolutional Networks through Network Slimming Liu et al., ICCV 2017
scaling是针对卷积的一种剪枝策略，我们对卷积操作后的每个通道都用一个 scaling factor 进行缩放。这个scaling factor就和其他参数一样是一个需要训练的参数。
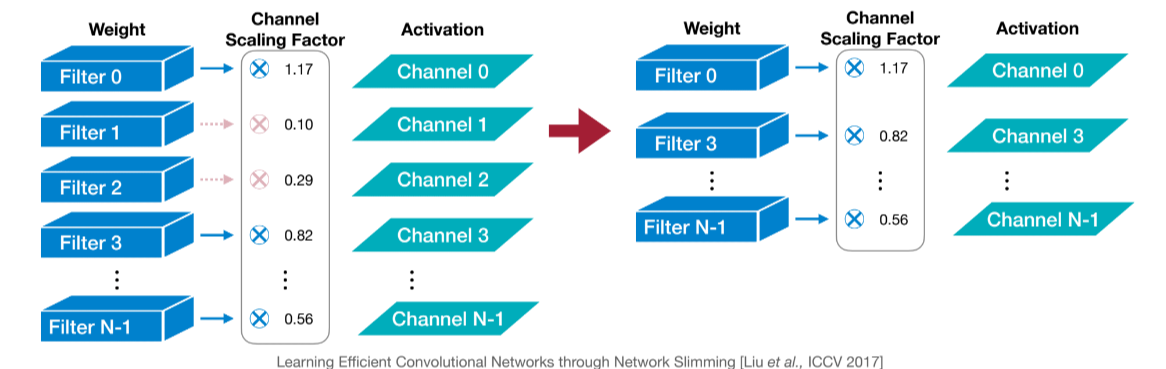我们在以scaling factor的大小代表这一channel的重要性，从而图中一样进行剪枝。事实上，我们并不需要额外的scaling factor，因为我们的batchnorm层有自带了一个scaling factor: $\gamma$ ($z = \gamma \frac{x - \mu}{\sqrt{\sigma^2 + \epsilon}} + \beta$)。我们可以直接用这个$\gamma$来进行剪枝。
Second-Order-based-pruning
Optimal Brain Damage LeCun et al., NeurIPS 1989
前面两种剪枝标准都是启发式的，通过定义参数的重要性进行剪枝。我们还可以通过 最小化剪枝前后的损失函数 来进行剪枝。 $$ \delta L = L(\mathbf{x}; \mathbf{W}) - L(\mathbf{x}; \mathbf{W}P = \mathbf{W} - \delta\mathbf{W}) = \sum{i} g_{i}\delta w_{i} + \frac{1}{2}\sum_{i} h_{ii}\delta w_{i}^2 + \frac{1}{2}\sum_{i \neq j} h_{ij}\delta w_{i}\delta w_{j} + O(|\delta\mathbf{W}|^3) \ where\ \ g_i = \frac{\partial L}{\partial w_i}, h_{ij} = \frac{\partial^2 L}{\partial w_i \partial w_j} $$ 这是LeCun在1989年时候的工作，它假设：
- 目标函数L是近似二次的，所以最后一项可忽略
- 这个神经网络的训练已经收敛了，这表明一阶导数（梯度）接近零，所以第一项 $(\sum_{i}g_{i}\delta w_{i})$ 也可忽略
- 删除每个参数引起的误差是独立的：这允许我们忽略混合二阶导数项 ，因为这些项描述的是参数之间的相互作用。
因此，我们可以得到： $$ \delta L_i = L(x; W) - L(x; W_p| w_i = 0) \approx \frac{1}{2}h_{ii} w_i^2 $$ 也就是$importance_{w_i} = |\delta L| = \frac{1}{2}h_{ii}w_{i}^2$，这就是一个二阶导数的剪枝标准。但是，由于$h_{ii}$ 是Hessian matrix，计算量过大，所以一般不会使用。
percentage-of-Zero-Based pruning
Network Trimming: A Data-Driven Neuron Pruning Approach towards Efficient Deep Architectures Hu et al.,ArXiv 2017
非常简单粗暴的对与Channel-level pruning的方法。由于Relu会产生0，我们直接定义每个通道的重要程度为其 Average Percentage of Zeros(APoZ)。选取最小APoZ的通道进行剪枝。
Regression-based pruning
Channel Pruning for Accelerating Very Deep Neural Networks He et al., ICCV 2017
regression-based pruning对于某一个layer进行操作，希望能够最小化重构误差。 令输入的feature map的channel数为$c$, 卷积核$W$的权重为 $n× c × k_h×k_w$, 卷积核每次卷积会在一个像素点上生成一个$N×n$的输出矩阵$Y$,其中$N$为batch_num，这里暂时不考虑bias项。要将$c$修剪为$c′$.同时最小化reconstruction error，这个优化问题是 $$ \begin{aligned} & \underset{\beta, W}{\text{arg min}} & & \frac{1}{2N} | Y - \sum_{i=1}^{C} \beta_i X_i W_i^T |_F^2 \ & \text{subject to} & & | \beta |_0 \leq C' \end{aligned} $$
其中$X_{i}$是一个$N \times k_h k_w$的矩阵裁剪自输入$X$。求解这个问题是NP难的,这里首先将问题用l1范数松弛为
$$ \begin{aligned} & \underset{\beta, W}{\text{arg min}} & & \frac{1}{2N} \left| Y - \sum_{i=1}^{C} \beta_i X_i W_i^T \right|_F^2 + \lambda \left| \beta \right|_1 \ & \text{subject to} & & \left| \beta \right|_0 \leq C’, ; \forall i, \left| W_i \right|_F = 1 \end{aligned} $$ 同时限制$||Wi||F=1$，然后在以下两个步骤中迭代
- 首先锁定$W$ ,求解$\beta$, 作为channel selection问题，这变成了零范数的LASSO regression。代码中可以知道作者是使用sklearn的Lasso regression函数做的
- 锁定$\beta$，问题变成了$\underset{W’}{\text{arg min}} \left| Y - X’(W’)^T \right|_F^2 $本质上是一个线性回归。
Pruning Ratio
对于不同的layer之间，怎么确定每个layer应该剪去多少的权重而不会过多的影响精度呢？
sensitivity of each layer
一种直观的方法就是查看每个layer对权重的敏感度各是多少，具体操作如下：
- 选定一个layer $L_i$
- prune $li$ with ratio $r_i \in {0.1, 0.2, …, 0.9}$(or other strides)
- 对每个ratio观察精度下降$\Delta Acc_r^i$
- 对所有layer重复上述操作
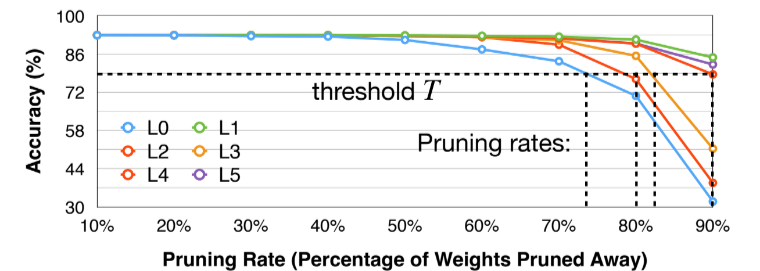图中是VGG-11在CIFAR-10数据集上的不同层的pruning ratio对精度的影响。选定一个threshold后就可以依据这个对不同layer选取不同的pruning ratio。
automatic pruning
上面的方法是一种手动的方法，并且没有考虑不同层之间的相互影响。 一个有意思的工作来自ECCV 2018, AMC: AutoML for Model Compression and Acceleration on Mobile Devices, 用了强化学习的方法来选取不同的pruning-ratio，效果很好。不过目前没看懂，后面有机会再补充。
Fine-tuning/Training
说了这么多pruing方法，具体的操作流程如下：
通常我们都会迭代式的再inference阶段进行pruning，例如，先采用50%的sparsity进行推理，得到精度误差后fine-tune一次，训练出新的weights分布，然后不断加大sparsity，不断重新fine-tune。如上图所示
System & Hardware Support for Sparsity
在pruning granularity的时候我们说到，若想要做到细粒度的剪枝，就需要特定的硬件支持。 韩老师自己的一篇论文[EIE](https://arxiv.org/pdf/1602.01528.pdfEIE: Efficient Inference Engine on Compressed Deep Neural Network)就支持对任意粒度的剪枝进行加速。由于我不是做硬件的，暂时没有仔细研究实现。
英伟达的Amper系列GPU也支持对于structured sparsity的加速，例如[N:M]剪枝。
架构图如下：
