TinyMl —— 模型量化(quantization)

Overview

模型量化（quantization）指的是用更少的bit表示模型参数，从而减少模型的大小，加速推理过程的技术。

一种常见的量化方式是线性量化(linear quantization)，也叫仿射量化(affine quantization)。其实就是按比例将tensor（一般为fp32）放缩到 $2^{bitwidth}$ 的范围内，比如8bit等。我们很容易给出量化公式： $$ r = s(q - z) $$ 其中，r(real value)值得是量化前的值，q(quantized value)是量化后的值，s(scale)是放缩比例，z(zero point)相当于是一个偏移量。

如何求出$s$和$z$呢？一种简单且常见的方式是通过最大最小值来估计，即：

$$ s = \frac{r_{max} - r_{min}}{q_{max} - q_{min}} $$ $r_{max}$就是这个tensor的最大值，$r_{min}$是最小值，$q_{max}$和$q_{min}$是我们指定的量化后的最大最小值。如下图所示：

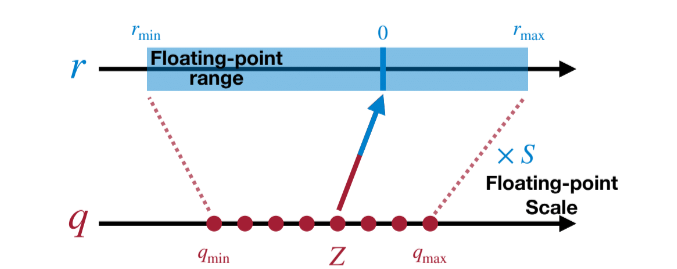
有了scale, 容易得到 $z = q_{min} - \frac{r_{min}}{s}$。在实际操作中，z一般会被round到最近的整数$z = round(q_{min} - \frac{r_{min}}{s})$（有很多不同的round规则，这个有具体实现决定）。

得到量化方程： $$ q = clip(round(\frac{r}{s}) + z, q_{min}, q_{max}) $$

代码示意如下：（实际会用pytorch已有的quantize api或者其他推理框架）

def get_quantized_range(bitwidth):
    quantized_max = (1 << (bitwidth - 1)) - 1
    quantized_min = -(1 << (bitwidth - 1))
    return quantized_min, quantized_max

def linear_quantize(fp_tensor, bitwidth, scale, zero_point, dtype=torch.int8) -> torch.Tensor:
    rounded_tensor = torch.round(fp_tensor / scale).to(dtype)
    shifted_tensor = rounded_tensor + zero_point
    quantized_min, quantized_max = get_quantized_range(bitwidth)
    quantized_tensor = shifted_tensor.clamp_(quantized_min, quantized_max)
    return quantized_tensor

上述过程被称为非对称量化(asymmetric quantization)。

还有一种对称量化(symmetric quantization)，它基于以下事实：常见的训练好的模型参数几乎总是关于0对称的。如下图所示：

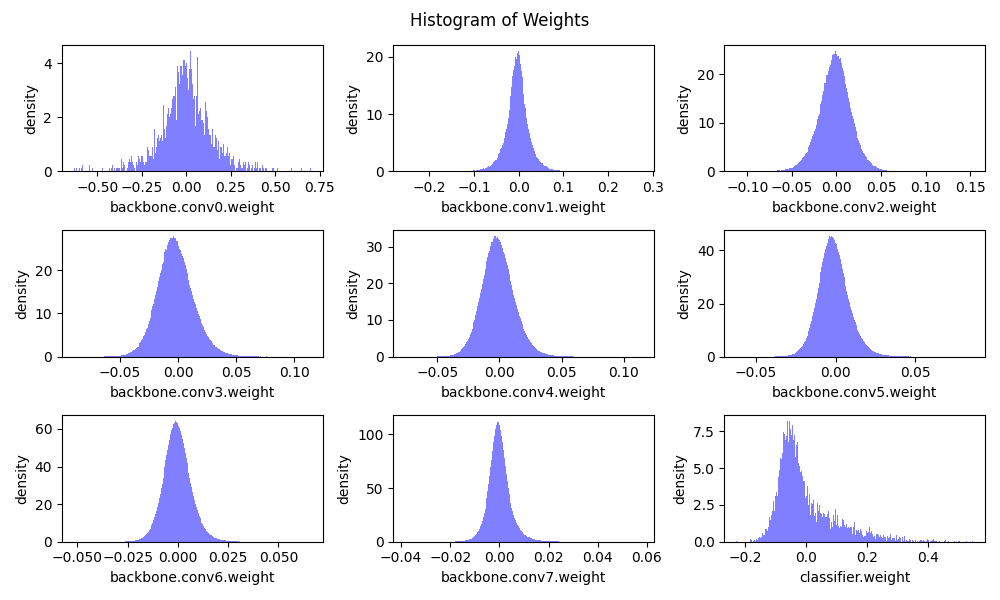
weight distribution

基于这个观察，我们常将zero point设置为0，并让 $q_{min} = -q_{max}$ 。这样，我们就可以简化量化公式为： $$ s = \frac{r_{max}}{q_{max}},\ \ z = 0 \ q = clip(round(\frac{r}{s}), -q_{max}, q_{max}), q_{max} = 2^{bitwidth - 1} - 1 $$ 这也是TensorRT等框架中常用的量化方式。

进一步的，当我们进行推理的过程中，对于一个全连接层，设$Y = WX$（暂不考虑bias），对左右两边都进行量化得到：

$$ \begin{align*} S_{Y}(q_{Y} - z_{Y}) &= S_{W}(q_{W} - z_{W})\cdot S_{X}(q_{X} - z_{x}) \newline q_{Y} &= \frac{S_{W}S_{X}}{S_{Y}}(q_{W} - z_{W})(q_{x} - z_{x}) + z_{Y} \newline q_{Y} &= \frac{S_{W}S_{X}}{S_{Y}}(q_{W}q_{x} - q_{W}z_{x} - z_{W}q_{x} + z_{W}z_{x}) + z_{Y} \newline q_{Y} &= \frac{S_{W}S_{X}}{S_{Y}}(q_{W}q_{X} - z_{X}q_{W}) + z_{Y}\ \ (assume\ z_{W} = 0) \newline \end{align*} $$

类似的，有bias的时候可以得到： $$ q_{Y} = \frac{S_{W}S_{X}}{S_{Y}}(q_{W}q_{X} - Q_{bias}) + z_{Y} \ \ \ (Q_{bias} = q_{b} - z_{X}q_{W}) $$ 根据卷积的线性可加性，我们也能有类似的结论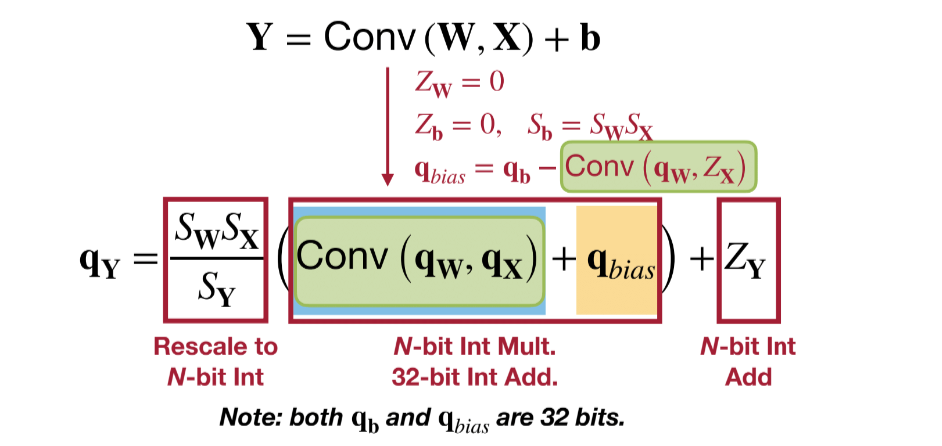： conv quantization 推理过程和全连接层类似，也可参见tinyml课程的lab2作业。

上式中，和 $W, b$ 相关的量化参数都可以容易被提前计算（训练好后对整个网络进行量化，记录所有weight, bias的量化值）。但对于$q_{X}， z_{X}$这种和输入相关的值，理论上来说是需要真正在设备上做推理的时候在能知道。但是如果我们每次做推理来一个input我们都对其做一个量化，这个开销是没法接受的。所以人们会用一个cablibration dataset，在做推理之前，在这个数据集上对所有的输入进行量化并得到一些量化参数，比如，cablibration dataset上的最大最小值，scale, zero point，以及$S_{Y}$等（具体过程见下文中的PTQ和QAT），以此当作推理时input的量化参数。

上述式子还存在两个问题

$\frac{S_{W}S_{X}}{S_{Y}}$是一个浮点数，我们不能让它参与计算。根据经验，这个结果一般都在(0, 1)之间，所以可以表示成$2^{-n}M_{0}$，其中$M_{0}$是一个整数，$n$是一个非负整数。这样我们就可以记录两个整数来代替浮点数。可以参见gemmlowp的实现
$q_{W} \cdot q_{X}$ 是很可能溢出 8bit的，所以其结果一般也会用32bit int表示（具体可能有不同的实现），所以我们一般也先将$Q_{bias}$量化为32bit int，便于与其结果相乘。最后需要对结果在量化为8bit int。

其他量化方法

minmax量化（$s = \frac{r_{max}-r_{min}}{q_{max} - q_{min}}$）有一个问题，也就是它容易受outlier的点的影响，这对模型参数的量化其实影响还好，因为参数的分布基本是对称的。但是对activations的结果就不一样了，所以又衍生出了几种量化方式。还记得上文说过，为了在模型真正部署之前得到对input, activations的量化参数，我们会在一个cablibration dataset进行训练。在这个过程中，我们可以通过取平均或者*指数移动平均(exponential moving averages)*的方式获取 $r_{max}, r_{min}$ ，从而减少outlier的影响。 $$ \hat{r}^{(t)}{max, min} = \alpha \cdot r^{(t)}{max, min} + (1 - \alpha) \cdot \hat{r}^{(t-1)}_{max, min} $$

TensorRT对activations的量化其实也是通过minmax方法，但是这个minmax是在一定阈值之内的minmax。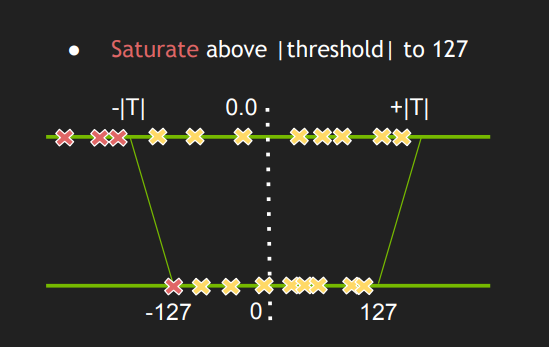那么如何确定这个阈值呢？我们肯定希望最小化量化前后数据分布的信息损失，这也是KL散度的思想。操作过程如下：

对于模型的每一层：

计算activations的直方图
选取多种threshold计算梁化后的分布与原分布的KL散度
选取最小KL散度对应的threshold 整个过程在典型的工作负载下大概需要几分钟。

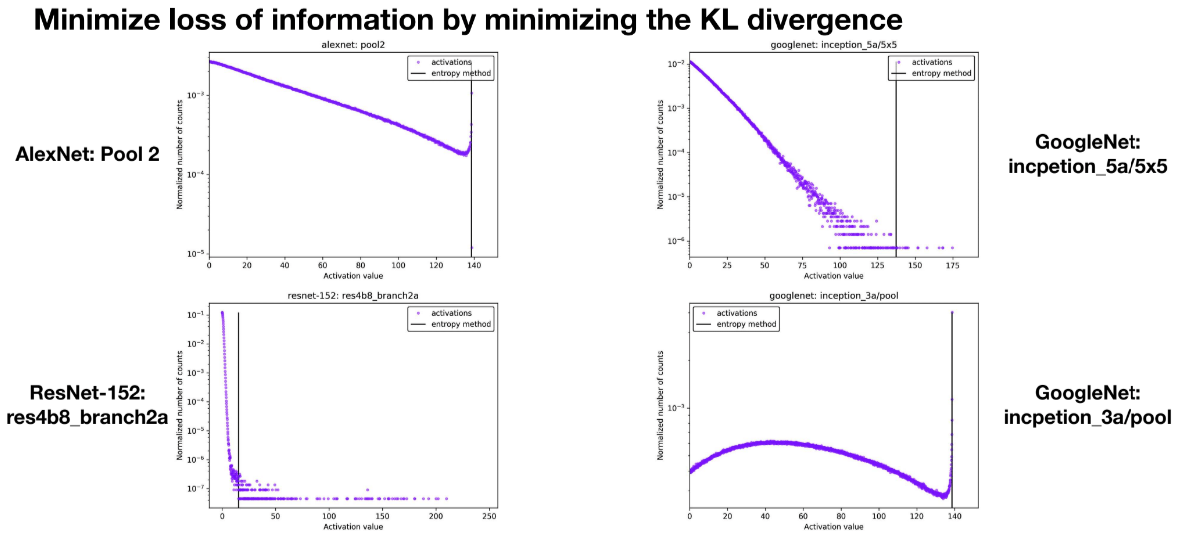
一些选取的threshold结果如下： tensorrt threshold

量化粒度

我们可以对每个tensor进行量化，也即对每个tensor都有一个scale和zero point。但人们发现，同一个tensor的不同channel的分布是很不一样的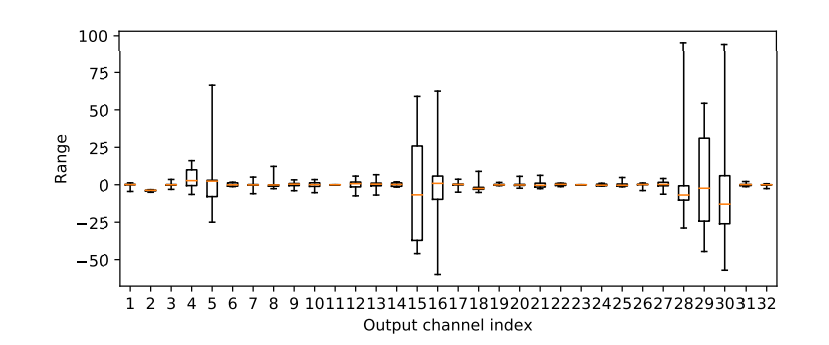： channel distribution 所以一个更细粒度的选择是进行per-channel量化，即对每个channel都有一个scale和zero point。

Post-training quantization(PTQ)

PTQ的过程比较简单，就是在训练后对模型进行量化。在这个过程前，我们还会用cablibration dataset来估计一些量化参数。流程如下： ptq

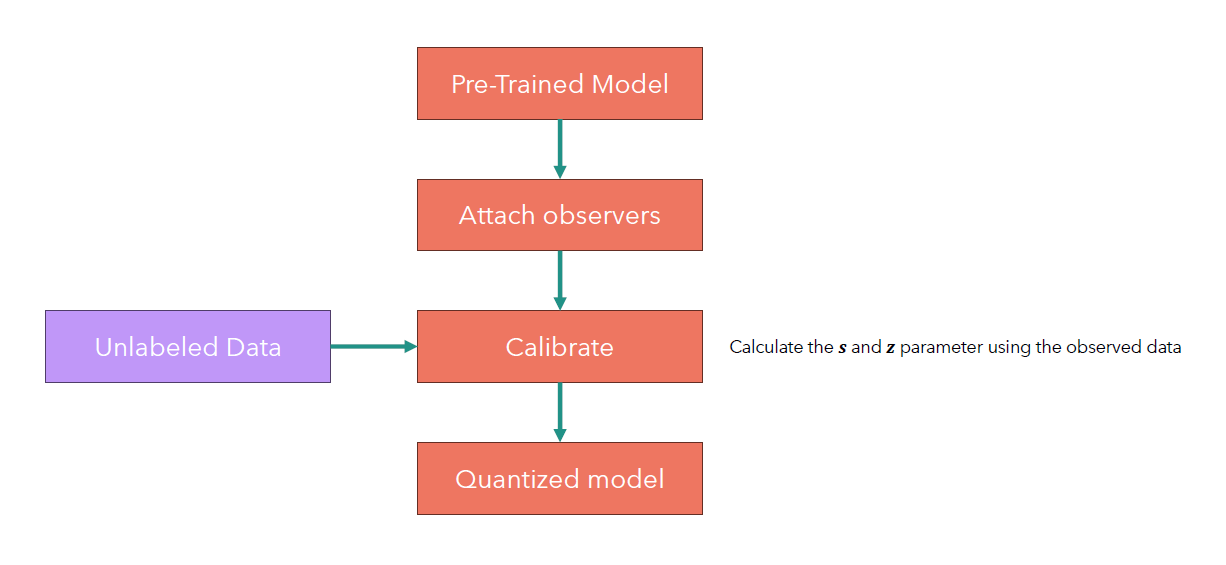
简单的pytorch代码如下：

class QuantizedSimpleNet(nn.Module):
    def __init__(self, hidden_size_1=100, hidden_size_2=100):
        super(QuantizedSimpleNet,self).__init__()
        self.quant = torch.quantization.QuantStub()
        self.linear1 = nn.Linear(28*28, hidden_size_1) 
        self.linear2 = nn.Linear(hidden_size_1, hidden_size_2) 
        self.linear3 = nn.Linear(hidden_size_2, 10)
        self.relu = nn.ReLU()
        self.dequant = torch.quantization.DeQuantStub()

    def forward(self, img):
        x = img.view(-1, 28*28)
        x = self.quant(x)
        x = self.relu(self.linear1(x))
        x = self.relu(self.linear2(x))
        x = self.linear3(x)
        x = self.dequant(x)
        return x
        
net_quantized = QuantizedSimpleNet().to(device)
# Copy weights from unquantized model
net_quantized.load_state_dict(net.state_dict())
net_quantized.eval()

net_quantized.qconfig = torch.ao.quantization.default_qconfig
net_quantized = torch.ao.quantization.prepare(net_quantized) # Insert observers
print(net_quantized)
# QuantizedVerySimpleNet(
#   (quant): QuantStub(
#     (activation_post_process): MinMaxObserver(min_val=inf, max_val=-inf)
#   )
#   (linear1): Linear(
#     in_features=784, out_features=100, bias=True
#     (activation_post_process): MinMaxObserver(min_val=inf, max_val=-inf)
#   )
#   (linear2): Linear(
#     in_features=100, out_features=100, bias=True
#     (activation_post_process): MinMaxObserver(min_val=inf, max_val=-inf)
#   )
#   (linear3): Linear(
#     in_features=100, out_features=10, bias=True
#     (activation_post_process): MinMaxObserver(min_val=inf, max_val=-inf)
#   )
#   (relu): ReLU()
#   (dequant): DeQuantStub()
# )

# 这次的测试实际上是做cablibration
test(net_quantized)
print(net_quantized)
# QuantizedVerySimpleNet(
#   (quant): QuantStub(
#     (activation_post_process): MinMaxObserver(min_val=-0.4242129623889923, max_val=2.821486711502075)
#   )
#   (linear1): Linear(
#     in_features=784, out_features=100, bias=True
#     (activation_post_process): MinMaxObserver(min_val=-53.58397674560547, max_val=34.898128509521484)
#   )
#   (linear2): Linear(
#     in_features=100, out_features=100, bias=True
#     (activation_post_process): MinMaxObserver(min_val=-24.331275939941406, max_val=26.62542152404785)
#   )
#   (linear3): Linear(
#     in_features=100, out_features=10, bias=True
#     (activation_post_process): MinMaxObserver(min_val=-28.273700714111328, max_val=20.937761306762695)
#   )
#   (relu): ReLU()
#   (dequant): DeQuantStub()
# )
net_quantized = torch.ao.quantization.convert(net_quantized)
print(net_quantized)
# QuantizedVerySimpleNet(
#   (quant): Quantize(scale=tensor([0.0256]), zero_point=tensor([17]), dtype=torch.quint8)
#   (linear1): QuantizedLinear(in_features=784, out_features=100, scale=0.6967094540596008, zero_point=77, qscheme=torch.per_tensor_affine)
#   (linear2): QuantizedLinear(in_features=100, out_features=100, scale=0.40123382210731506, zero_point=61, qscheme=torch.per_tensor_affine)
#   (linear3): QuantizedLinear(in_features=100, out_features=10, scale=0.3874918520450592, zero_point=73, qscheme=torch.per_tensor_affine)
#   (relu): ReLU()
#   (dequant): DeQuantize()
# )

在实际的部署中，一般不会用pytorch的量化模块。根据你所需要的后端，选择tensorrt, onnxruntime, openvino, ncnn等框架的量化模块。

Qauntization-aware training(QAT)

qat顾名思义，指的是开模型训练的前就将模型进行量化，从而训练出来的误差更接近“量化误差”。但人们经过广泛的时间发现，将一个训练好的模型在量化后进行微调，要比量化模型在从零训练的准确率更高。所以现在的qat的training一般指的是微调量化模型。在pytorch中的流程基本和PTQ差不多，就是训练时改成

net.train()
net_quantized = torch.ao.quantization.prepare_qat(net) # Insert observers

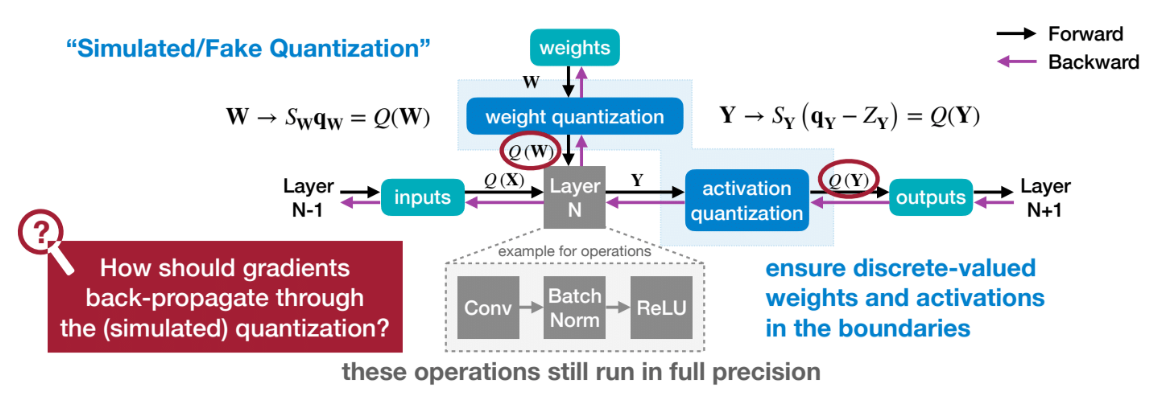
但是其原理不同，因为涉及到了反向传播的过程。QAT的流程如下： quantization aware training

在qat的过程中，我们会保存一份fp32的weight副本，这是用来更新梯度的（若只有梁化后的int8 weight，我们每次的梯度变化会在round的时候被归零，例如，weight是3.2， quantized weight是3，这次反向传播的时候需要剪去0.1，如果quantized weight - 0.1在round之后还是3，所以我们需要保留原来的fp32 weight, 不断累积梯度更新，当累计一定值后，quantized weight就会被更新了）。

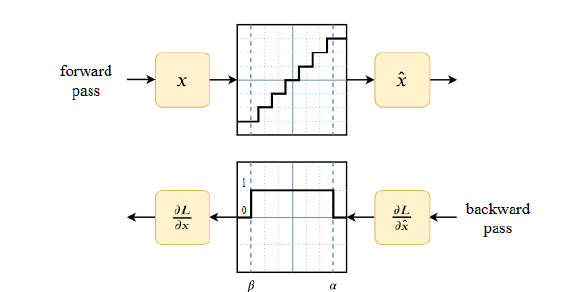
在反向传播过程中，模型需要对每个权重和输入计算损失函数的梯度。这里出现了一个问题：我们之前定义的量化操作的导数是什么？实际上量化得到的结果是离散值，所以导数应该在任何地方都是0， $\frac{\partial Q(W)}{\partial W} = 0$，如果我们这个设置，网络什么也学不到因为梯度得不到更新。一个典型的解决方案是使用Straight-through Estimator，简称STE，来近似这个梯度。STE简单的将量化操作的导数设置为1，即$\frac{\partial Q(W)}{\partial W} = 1$。这样，我们就可以在反向传播的过程中更新梯度了。为什么能设置成1呢，因为实际上这是一个阶梯函数，如下图所示： ste

reference

tinyml quantization
Quantizing deep convolutional networks for efficient inference: A whitepaper
gemmlowp关于量化的示例
8-bit inference with TensorRT

Overview#

其他量化方法#

量化粒度#

Post-training quantization(PTQ)#

Qauntization-aware training(QAT)#

reference#