Icpc

没写记录，学弟写了，直接用 ICPC西安邀请赛

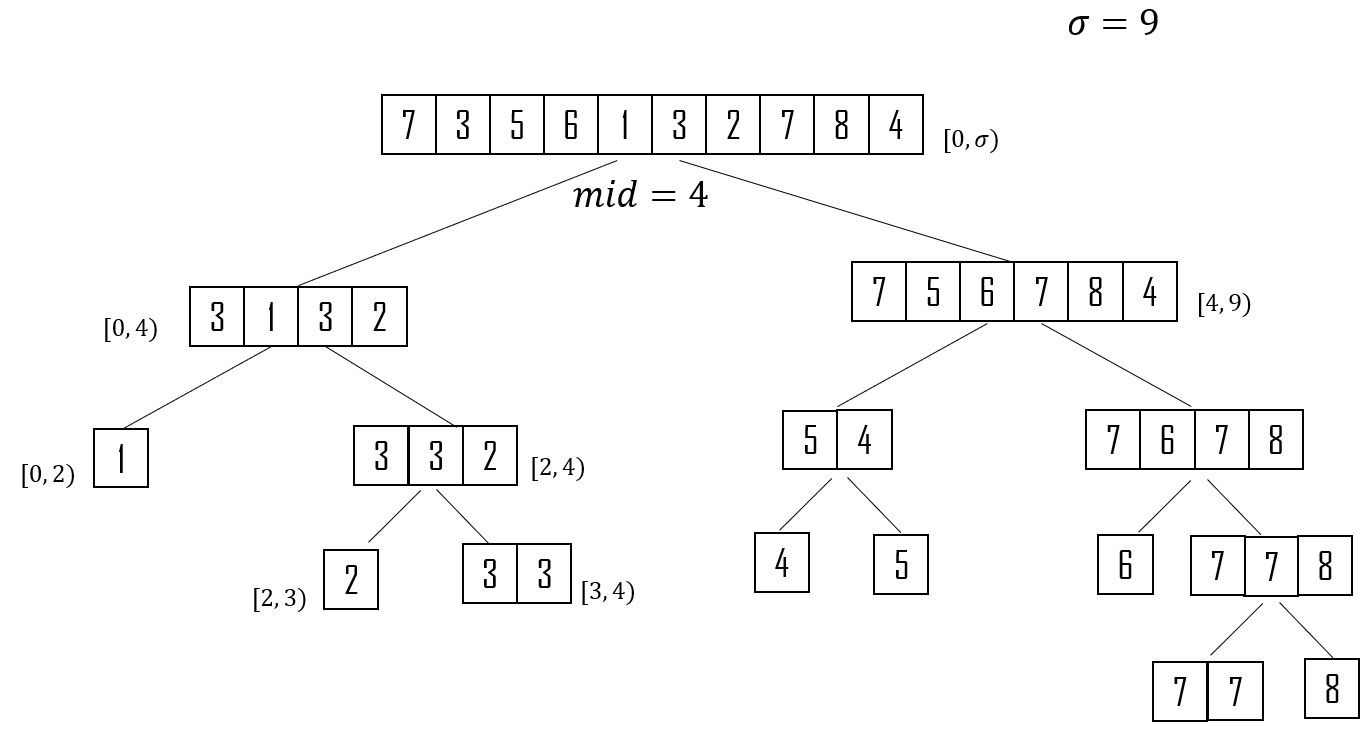
Wavelet Tree for Competitive Programming 最近在学FM-Index相关算法用于数据库，了解到Wavelet Tree这一数据结构，发现其还可以应用在算法竞赛中。网上相关中文资料比较少，权当自己做个学习笔记 开始之前 在学习wavelet tree前，不妨看看他能解决什么样的问题。 假设我们有一长为 $n$ 的序列 $A[0…n - 1]$ 。在算法竞赛中，典型的数据量是 $n = 1e5, |A[i]| <= 1e9$ 区间 $[L, R)$ 中元素$x$的出现次数 区间 $[L, R)$ 中的第k小数 区间 $[L, R)$ 上 小于等于x的数的个数 … 以上问题都可以通过可持久化线段树在解决。那为什么还需要wavelet tree呢，我们都知道可持久化线段树的常数很大，并且十分消耗空间，在有些苛刻的题目下可能会被卡 好吧应该都是金牌题，不是我该考虑的 。利用wavelet tree可以在$log(\sigma)$时间内完成的同时（且优秀的常数），若使用bitvector优化空间，空间上大概比可持久化线段树少一个量级。最重要的一点是，我个人觉得他比主席树更加直观易懂。 $\sigma$ = | $\Sigma = {1, 2, \cdots, \sigma}$| （用于序列上时是值域大小）。 用wavelet tree的缺点就是带修改操作比较难写，码量较大，一般不会在比赛时使用。 Wavelet Tree 该图给出了用序列 $A = [7, 3, 5, 6, 1, 3, 2, 7, 8, 4]$ 构建的wavelet tree的形态。对于树上的每个节点，我们会将其按照值域分成两个部分$[low, mid), [mid, high)$。通过 稳定划分（stable_partition，即不改变相对顺序的情况下划分）将该节点上的序列中小于 $mid$的划分到左子树中，大于等于mid的划分到右子树中，递归直至节点中只有一种值时为叶节点。需要注意的是，我们并不会在叶子节点中直接存储序列的值，而是通过某个方法使得我们能够使用较小的空间的情况下得到足够的信息。 ...

icpc模板 Previous Next     / [pdf] View the PDF file here. algorithm-template Competitive Programming template ...